Una porta per trovarle tutte

Cara lettrice, caro lettore,

oggi parliamo ancora di porte logiche, raccontandovi una curiosità matematica che ha applicazioni pratiche incredibili nell’elettronica. Abbiamo già visto in una puntata precedente come le porte logiche si possano interpretare come funzioni, e come queste funzioni possano essere composte tra di loro in modo da ottenere altre funzioni. Così come la funzione (x+1)^2 si può ottenere componendo f(x)=x^2 e g(x)=x+1 in modo opportuno, così per esempio A XOR B = (A OR B) AND (NOT(A AND B)). Provate a verificarlo costruendo la tabella di verità.

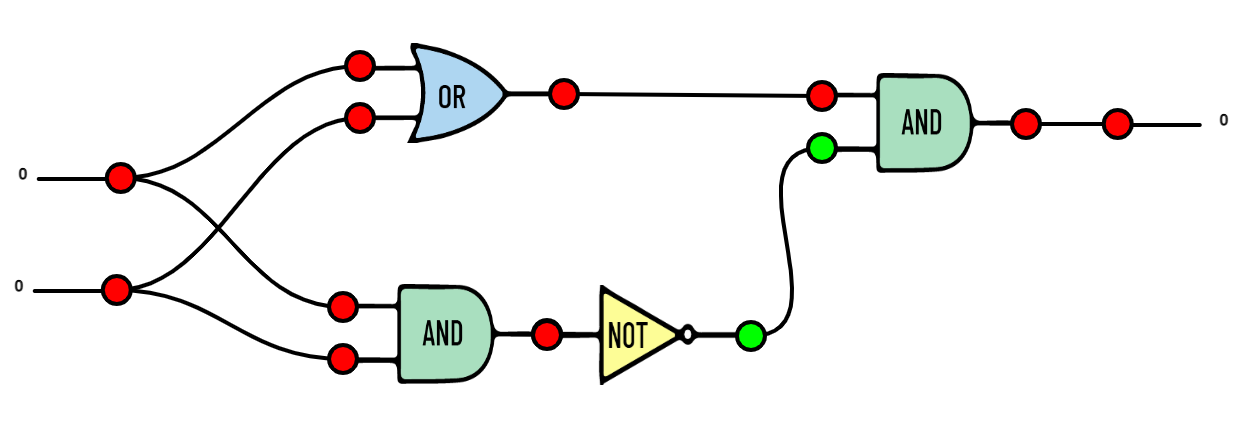Una costruzione alternativa della porta logica XOR. Notate che questa costruzione non è unica, la porta XOR si può realizzare anche in altro modo usando AND, OR e NOT. Vi ricordate come?

Questo esempio ci fa osservare che potremmo costruire la porta logica XOR avendo a disposizione come mattoncini di partenza le porte logiche OR, AND e NOT. Ora ci occuperemo di una costruzione simile, usando una porta logica particolare chiamata NAND. Questa porta logica è si può costruire negando l’output di una porta logica AND. Possiamo cioè dire che A NAND B = NOT(A AND B). Tuttavia, da adesso in avanti la utilizzeremo come mattoncino fondamentale, senza ricordare come è stata costruita, ma solo ricordando la sua tabella di verità: Falso, quando entrambi gli input sono Veri, e Vero in tutti gli altri casi.

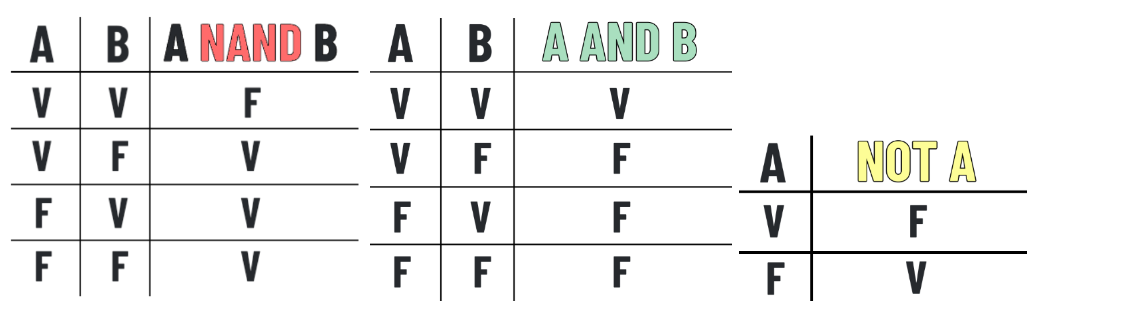La tavole di verità delle porta logiche NAND, AND e NOT

Come mai siamo così interessati alla porta logica NAND? Il motivo è che questa, insieme alla porta logica NOR (la negazione di OR) è una porta logica universale. Cioè, tutte le altre porte logiche si possono ottenere componendo in modo opportuno diverse copie della porta NAND. Matematicamente, questo è un risultato che affonda le sue radici nell’algebra booleana. Dal punto di vista pratico, ci permette di realizzare molti circuiti partendo da un solo chip che contiene porte logiche NAND (https://en.wikipedia.org/wiki/7400-series_integrated_circuits).

Ora è il momento di provare a dimostrare quello che abbiamo affermato, e per farlo si deve semplicemente provare a costruire le porte logiche AND, NOT, OR, XOR, usando solo il mattoncino fondamentale che chiameremo NAND. Ci basterà quindi fare degli esempi per confermare il nostro primo risultato. Osservate però che, sebbene ci si limiti a fare degli esempi, non vuol dire che non si debba usare il ragionamento: sappiamo già che la porta XOR si può ottenere con AND, OR e NOT. Quindi, se siamo in grado di costruire queste tre porte usando NAND, possiamo costruire anche XOR, sostituendo le configurazioni con i NAND nella formula A XOR B = (A OR B) AND (NOT(A AND B)).

La prima costruzione riguarda la porta logica NOT. In questo caso, sperimentando la costruzione con una sola porta logica NAND il risultato è chiaro già guardando la tavola di verità: V NAND V = F e F NAND F = V. Quindi possiamo “collegare insieme” gli input della porta logica NAND per ottenere il NOT: NOT(A) = A NAND A.

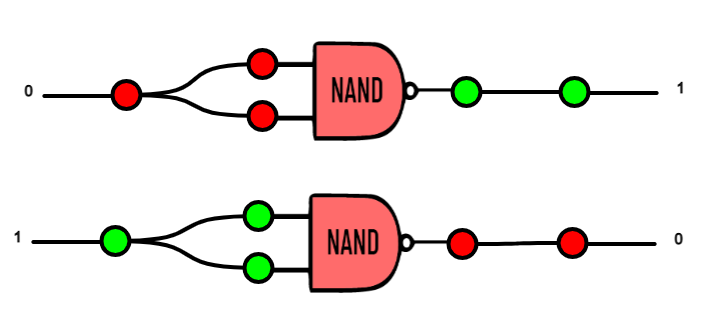La porta logica NOT costruita usando una porta logica NAND

Una volta ottenuto il NOT, è molto facile ottenere la porta AND: ricordandoci originariamente che NAND si può costruire negando l’output di una porta AND, possiamo negare un’ulteriore volta questo output e ottenere la porta AND. In formule, sappiamo che NOT(A NAND B) = A AND B, e inoltre sappiamo costruire il NOT usando solo NAND. Per cui otteniamo A AND B = (A NAND B) NAND (A NAND B).

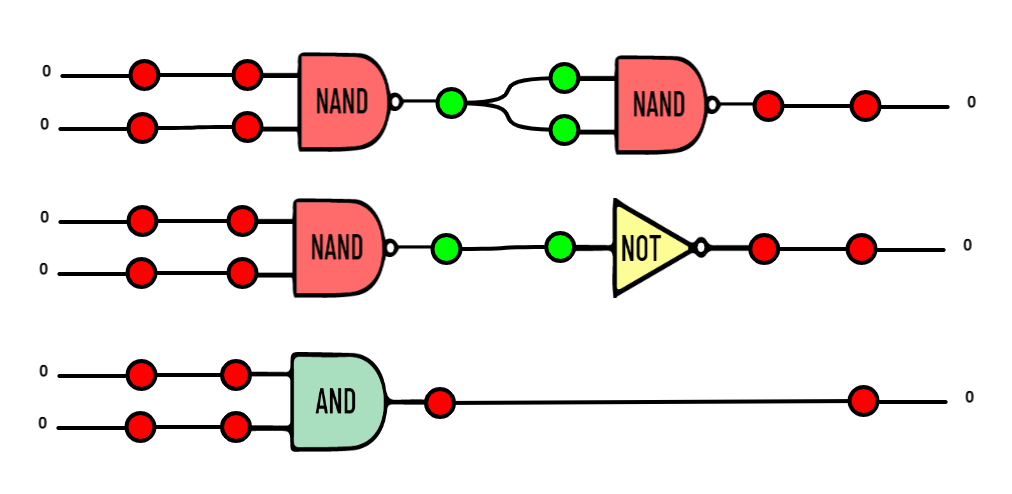Sulle tre righe, la ricostruzione delle operazioni che ci hanno portato a costruire AND usando solo NAND. Prima si scrive AND usando NAND e NOT, e poi usando la costruzione del NOT vista in precedenza.

Avendo a disposizione le porte logiche AND e NOT, è il momento di costruire l’OR. Anche in questo caso il risultato si può ottenere in due modi: il primo è quello di “giocare” un poco accostando porte NAND e ricavando il risultato finale; con un po’ di fantasia è possibile ottenere il risultato voluto. L’altra possibilità è osservare che le porte logiche OR e NAND hanno una tabella di verità molto simile, semplicemente NAND è falsa se e solo se entrambi gli input sono veri, e OR è falsa se e solo se entrambi gli input sono falsi.

La tavole di verità delle porta logiche NAND, e OR

Da questo si ricava che per costruire l’OR basta negare entrambi gli input di una porta NAND, e viceversa. In formule: A OR B = (NOT A) NAND (NOT B), o viceversa A NAND B = (NOT A) OR (NOT B). E pensandoci ancora un po’, questo deriva semplicemente dall’osservazione che negare una proposizione in cui compare OR fa comparire NAND, argomento che abbiamo già affrontato. Abbiamo trovato che

A OR B = (A NAND A) NAND (B NAND B)

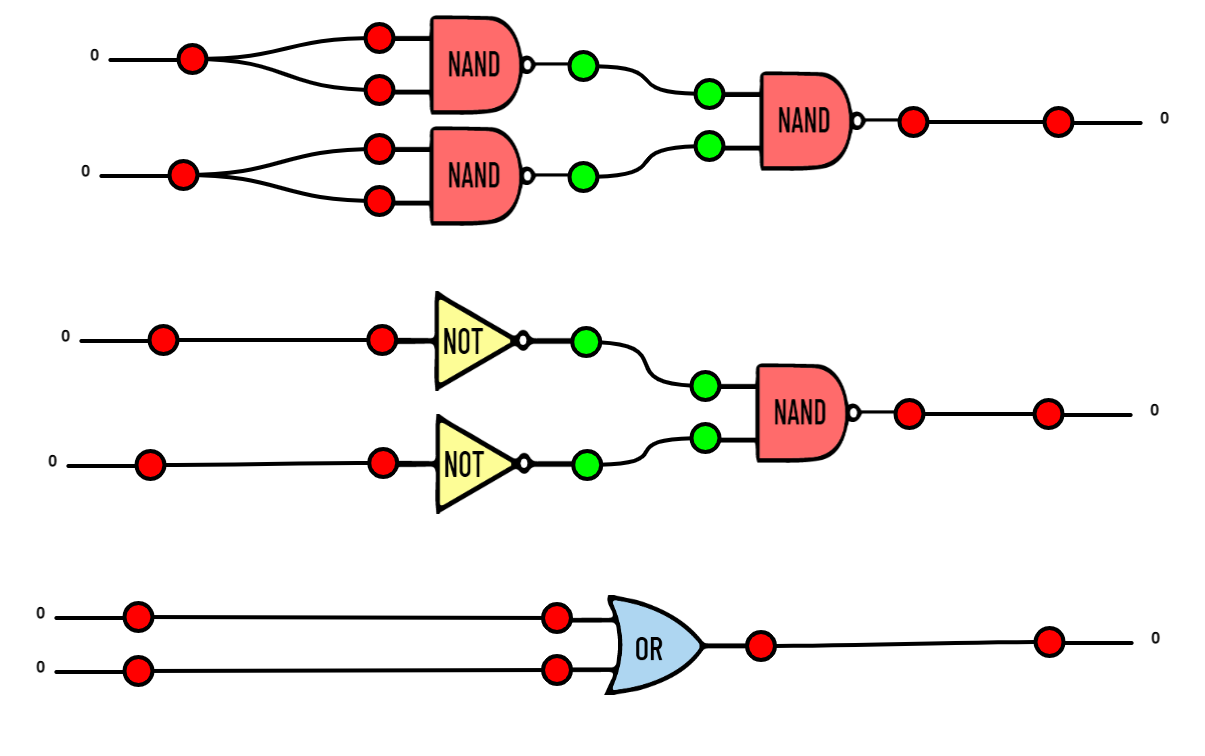Sulle tre righe, la ricostruzione delle operazioni che ci hanno portato a costruire OR usando solo NAND. Prima si scrive OR usando NAND e NOT, e poi usando la costruzione del NOT vista in precedenza.

Con questo abbiamo terminato: abbiamo dimostrato con esempi che è possibile utilizzare solo la porta NAND per costruire AND, OR, NOT (e XOR). Questa è una possibile definizione di porta logica universale. Si può dire molto di più e dimostrare che usando NAND si possono costruire tutte le funzioni binarie con un numero arbitrario di input e output, ma questo richiede un procedimento più ingegnoso. Vi lasciamo sfidandovi a ripetere queste costruzioni usando la porta logica NOR.

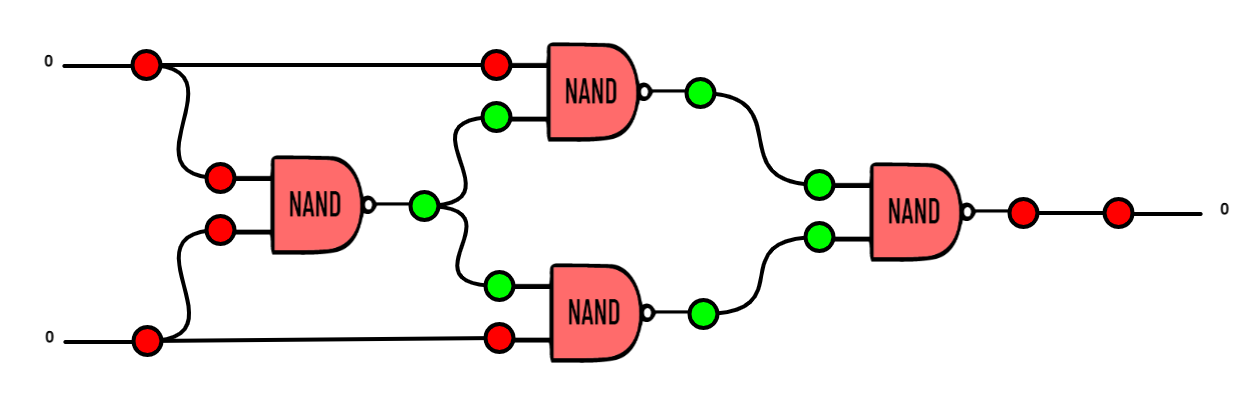Un modo per costruire XOR usando NAND. Riuscite a trovarne altri?