Cosa proporre negli ultimi giorni di scuola quando la stanchezza e il caldo iniziano a farsi sentire? Ovviamente attività interessanti e coinvolgenti, ma anche utili per consolidare gli argomenti già affrontati o per esplorare in maniera ludica nuovi aspetti da approfondire successivamente.
La proposta didattica di questo articolo riguarda un colorato completo estivo origami, da realizzare con poche e semplici pieghe.
Uno degli aspetti interessanti degli origami è la varietà delle attività che posso essere proposte a partire da un foglio di carta. Ogni modello può essere analizzato da più punti di vista e in diversi momenti. Si possono fare osservazioni mentre si piega, sul modello finito o sul foglio delle pieghe, il crease pattern, che si ottiene riaprendo il modello origami dopo l’ultima piega. Si possono osservare le diverse figure geometriche che si formano tra le pieghe, la loro area, il loro perimetro, i loro lati o i loro angoli, ecc.
Come gli altri modelli, anche il completo estivo origami, offre diversi spunti didattici. In particolare, in questo articolo, ci soffermeremo sul crease pattern, esplorando le possibili domande da rivolgere ai bambini.
Il completo estivo origami
Per realizzare il completo estivo (scarica le istruzioni) si consiglia di utilizzare un foglio origami bicolore (già pronto o da realizzare colorando in modo diverso le due facce del foglio) in modo tale da differenziare il colore della maglietta da quello del pantaloncino.
Dopo aver effettuato l’ultima piega, riapriamo delicatamente il foglio fino a tornare al quadrato di partenza e ripassiamo con un colore le pieghe visibili: otterremo il crease pattern allegato.
Vediamo ora quali particolarità nasconde il crease pattern del completo estivo.
Possiamo iniziare osservando e classificando le diverse forme.
In quante figure è suddiviso il foglio? Quali figure geometriche riconosci?
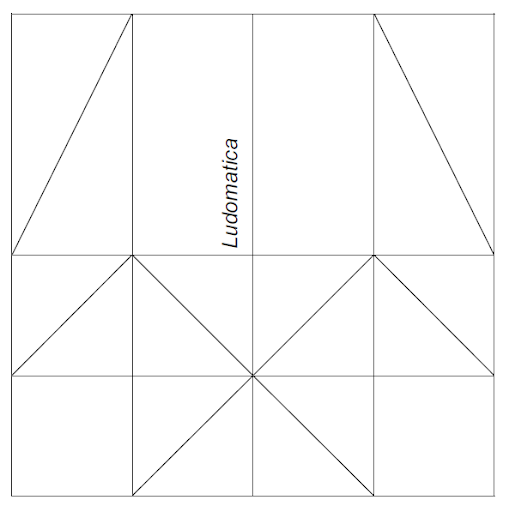
Il quadrato iniziale è ora suddiviso in 20 figure geometriche: 2 rettangoli, 2 quadrati e 16 triangoli (4 triangoli rettangoli scaleni e 12 triangoli rettangoli isosceli). Si può chiedere di colorare le diverse figure geometriche con colori differenti (es. giallo = triangolo, rosso = quadrato, blu = rettangolo).
Spostiamo ora l’attenzione sulla superficie delle diverse forme.
Quali figure occupano la stessa superficie?
È interessante osservare che ci sono due triangoli non equiestesi e che ci sono figure differenti (es. triangolo rettangolo scaleno e quadrato) che hanno la stessa area. Colorando con lo stesso colore le figure equiestese emergeranno tre diverse aree che potremmo esprimere anche sotto forma di frazione: rettangolo 1/8, quadrato e triangolo rettangolo scaleno 1/16, triangolo rettangolo isoscele 1/32. La particolarità di questo crease pattern riguarda anche il rapporto tra le aree delle diverse figure: l’area del quadrato è il doppio di quella del triangolino e la metà di quella del rettangolo. Assegnando ad ogni figura la relativa frazione, è possibile effettuare anche delle semplici addizioni tra frazioni con l’aiuto del supporto visivo: una figura creata unendo un quadrato e un rettangolo corrisponde, ad esempio, a 3/16 del quadrato iniziale, ovvero 1/16 + 1/8.
Possiamo infine ritagliare le diverse forme del crease pattern e utilizzarle come tessere di un puzzle per comporre altre figure.
Il quadrato iniziale, il castello, il cono e la barca sono figure equiestese?
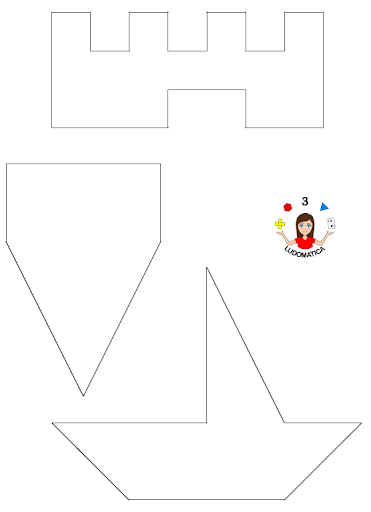
Dopo aver ritagliato il crease pattern, i bambini utilizzano tutte le forme geometriche per comporre ogni figura (vedi allegato). Oltre ad essere una sfida divertente, giocando i bambini potranno constatare che le varie figure occupano la stessa superficie perché equiscomponibili.
Gli spunti didattici non si esauriscono qui: si può continuare a giocare con il completo estivo origami esplorando la simmetria nel crease pattern o nel modello finito oppure divertirsi con il calcolo combinatorio scoprendo quanti completi differenti si possono creare con tre diversi colori (es. rosso, giallo e blu) e come posizionare il foglio di partenza per ottenere la maglietta e il pantaloncino di un determinato colore.
Buone pieghe e buon divertimento!