Cara lettrice, caro lettore,
oggi parliamo di porte logiche: elementi fondamentali dell’elettronica digitale che sottendono ogni operazione svolta da un computer, le cui proprietà si possono studiare approfonditamente usando il linguaggio matematico. Da questo punto di vista, possiamo immaginare le porte logiche come fossero funzioni: hanno un certo numero di variabili, o input, che possono valere {0, 1}, o {falso, vero}, e restituiscono un certo numeri di valori, anch’essi {0, 1}. Oggi parleremo di porte logiche unarie e binarie, cioè con uno o due input rispettivamente, e un solo output: di fatto le più semplici possibili. Queste costruzioni logiche sono così comuni, semplici ed eleganti, da ritrovarsi anche molto spesso nel linguaggio quotidiano. Analizziamo quindi queste strutture e i paralleli tra logica matematica e lingua italiana.
Le porte logiche AND, OR, XOR e NOT sono il “vocabolario base” dei circuiti digitali. La porta AND restituisce vero (1) solo se tutti gli ingressi sono veri (1), e falso (0) altrimenti. In termini linguistici, “la spiaggia è aperta quando il mare è calmo E c’è il sole” significa che entrambe le condizioni devono essere soddisfatte affinché la spiaggia sia aperta. In termini matematici, potremmo descrivere la funzione f(x,y) = x AND y, come la funzione f(x,y) = min(x,y). Ma ci sono modi più eleganti di ottenere questo risultato, restringendo la nostra aritmetica a utilizzare solamente i valori 0 e 1.
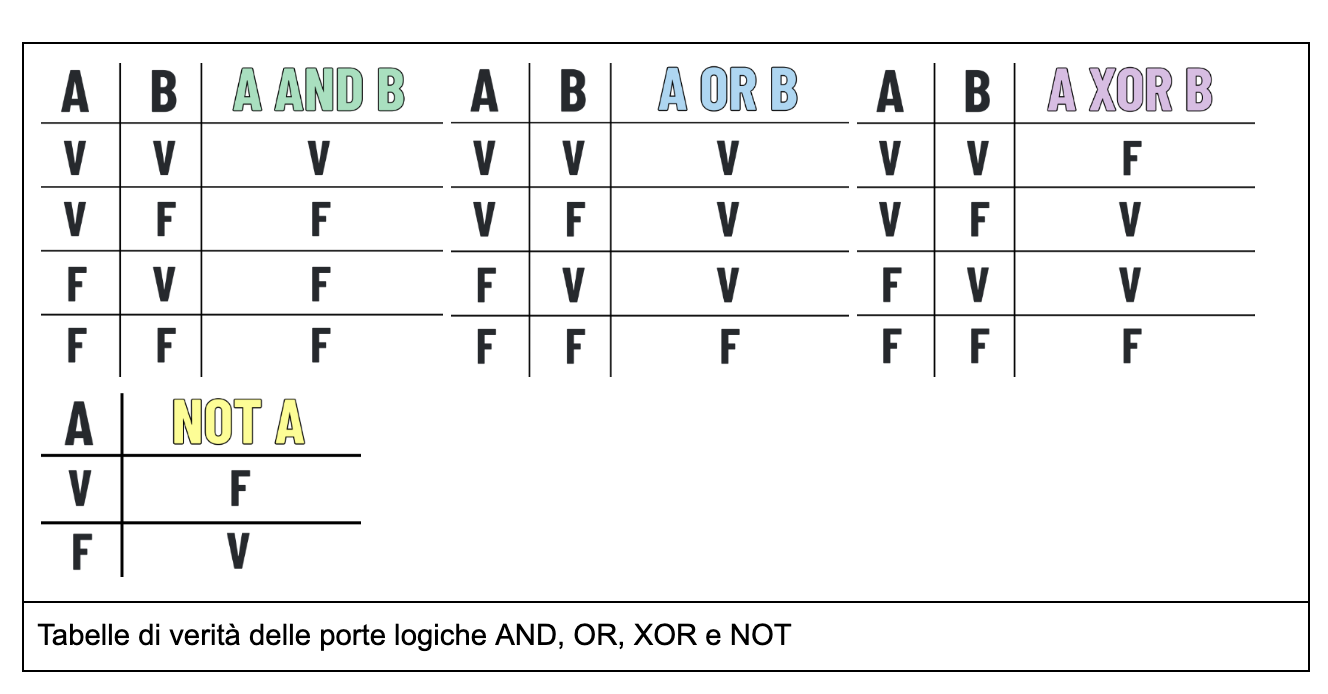
La porta OR restituisce vero se almeno un ingresso è vero. Linguisticamente, “la partita viene annullata in caso di pioggia O di vento forte” ci dice che la presenza di almeno una delle due condizioni comporta l’annullamento della partita. In termini matematici, potremmo descrivere la funzione f(x,y) = x OR y, come la funzione f(x,y) = max(x,y).
La porta XOR, o OR esclusivo, restituisce vero solo se gli ingressi sono diversi tra loro. Questo trova riscontro nella frase “ci troviamo alla stazione O nella piazza principale del paese”, sottintendendo che ci si possa trovare in un solo luogo alla volta. In termini matematici, potremmo descrivere la funzione f(x,y) = x XOR y, come la funzione f(x,y) = |x-y|.
L’operatore NOT è una negazione, trasformando vero in falso e viceversa. Concettualmente è il più semplice, ma le sue implicazioni possono essere profonde quando combinato con altri operatori. In termini matematici, potremmo descrivere la funzione f(x) = NOT x, come la funzione f(x) = 1-x.
Le funzioni possono essere composte tra di loro, cioè eseguite una di seguito a un’altra, facendo in modo che gli output della prima funzione coinvolta diventino gli input della seconda. Questo fenomeno si ritrova anche nella lingua italiana, quando si costruiscono delle frasi subordinate, che diventano componenti di altre frasi. Usiamo la composizione per descrivere in un altro modo la porta logica XOR: la tavola di verità di P XOR Q è la stessa che si ottiene da (P AND (NOT Q)) OR (Q AND (NOT P)).
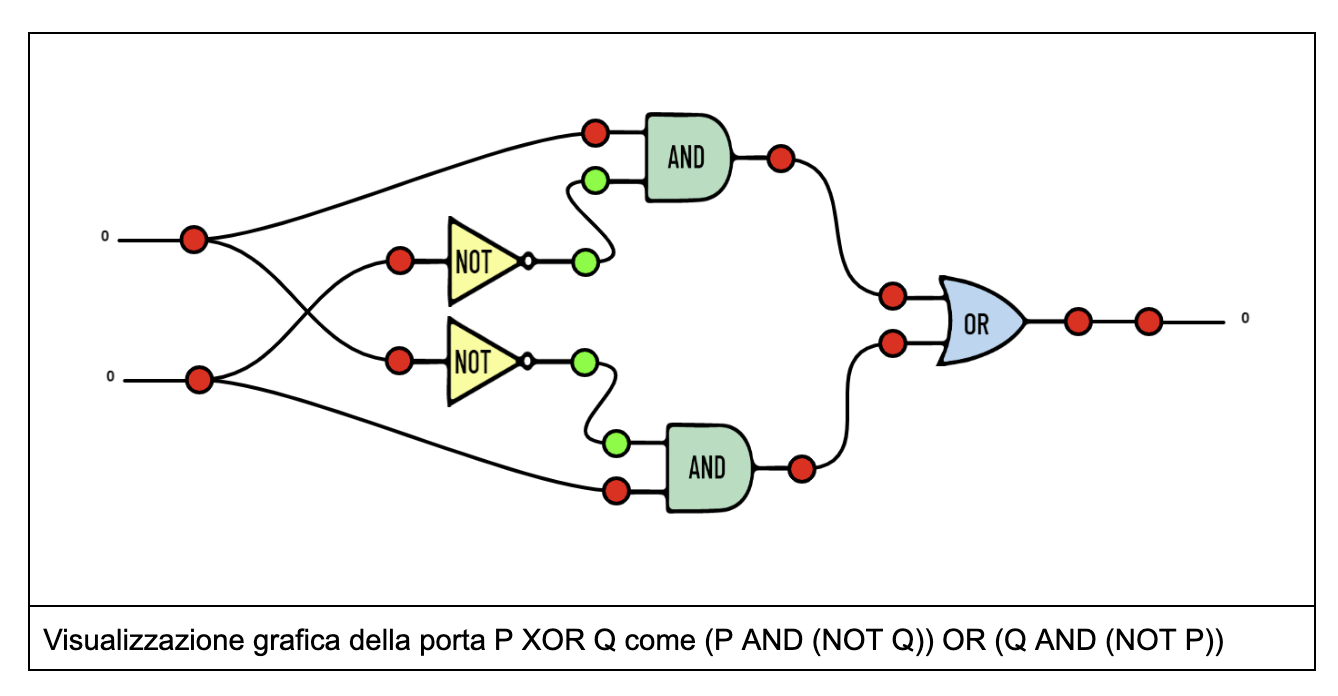
In pratica, questo significa che in una scelta esclusiva, come “ci troviamo alla stazione O nella piazza principale del paese”, stiamo in realtà dicendo “ci troviamo alla stazione E non ci troviamo in piazza, OPPURE ci troviamo in piazza E non ci troviamo alla stazione”. Provate a riscrivere in questo modo il detto “O mangi la minestra O salti dalla finestra”.
Approfondiamo ora la negazione di un operatore. Dalla proposizione “la spiaggia è aperta quando il mare è calmo E c’è il sole”, deduciamo che, quando la spiaggia non è aperta, deve essere vero che il mare NON è calmo OPPURE NON c’è il sole. Questo concetto viene espresso come (NOT P) OR (NOT Q). Similmente, negando P OR Q, e sapendo che “la partita viene annullata in caso di pioggia O di vento forte”, se la partita è stata effettuata, allora non ci deve essere stata né pioggia né vento forte. Esprimiamo questo concetto come (NOT P) AND (NOT Q), trovando un corrispettivo più diretto nella nostra lingua grazie alla costruzione “né…né…”.
Questi esempi provengono dalla mostra “Circuiti invisibili” di Curvilinea, che esplora le applicazioni delle porte logiche da varie angolazioni, inclusi linguaggio e matematica, ma facendo anche ponti verso il mondo dell’informatica. Insegnanti, vi incoraggio a scoprire insieme agli studenti come, dalle sabbie digitali dei chip ai fili della comunicazione, i fondamenti della logica matematica e la struttura della nostra lingua si incrociano e si rafforzano a vicenda, dimostrando ancora una volta la meravigliosa intrecciatura tra matematica e realtà.