Ragionare sull’incerto
Quando si introducono gli studenti alla probabilità, è sempre bene tenere a mente un fatto: ragionare di probabilità è difficile. Non si tratta solamente dell’impressione di chi scrive o di quella dei molti che si cimentano nell’impresa, ma è la conclusione a cui sono giunti negli anni numerosi studi, svolti principalmente allo scopo di indagare il modo in cui prendiamo decisioni in situazioni incerte. Psicologi del calibro di Daniel Kahneman (Premio Nobel per l’economia nel 2002 proprio per l’impatto dei suoi lavori in ambito economico), Amos Tversky e Gerd Gigerenzer hanno fornito spiegazioni diverse: se da un lato i primi due sostengono l’ipotesi secondo cui, per natura, la mente umana sia poco adatta al ragionamento probabilistico e invece maggiormente incline al pensiero intuitivo, l’ultimo punta invece il dito contro la nostra ignoranza in materia.
Una competenza cruciale
Qualunque sia la spiegazione, è però evidente che saper riconoscere e limitare l’influenza delle fallacie dell’intuizione in situazioni incerte è una competenza essenziale per un cittadino: saper gestire razionalmente la probabilità serve a interpretare dati ed informazioni oltre che a orientare attivamente le proprie decisioni in scenari aleatori. Diventa quindi particolarmente opportuno togliere alla probabilità quel ruolo di Cenerentola della programmazione disciplinare ed evitare di riservarle quello di prima vittima sacrificale in caso di imprevisti o ritardi.
Prendere il toro per le corna
Un nodo cruciale rimane dunque come portare alla luce queste difficoltà senza spaventare gli studenti che incontrano la probabilità al termine del primo ciclo, per i quali la capacità di astrazione è spesso ancora non completamente costituita. Si tratta più che altro di preparare il terreno a quello che poi dovrà essere formalizzato più sistematicamente in studi superiori, cercando di costruire un’idea di probabilità priva di misconcezioni e provando tuttavia a non nascondere le difficoltà che emergono nel trattare tali argomenti.
Un modo per farlo potrebbe essere proprio prendere il toro per le corna ed esporre deliberatamente gli studenti a problemi dai risultati sorprendenti e controintuitivi, che, se opportunamente presentati, possano alimentare la convinzione che una trattazione ragionata dei fenomeni aleatori sia tanto utile quanto necessaria. Non si tratta ovviamente solo di motivare l’apprendimento, ma anche di esporre sin da subito le insidie di cui è costellato il tema.
Il ruolo del coding con Scratch!
In un percorso di questo genere, un linguaggio di programmazione come Scratch! può rappresentare uno strumento efficace per comprendere problemi poco intuitivi oppure per costruire esperimenti aleatori di una certa complessità, la cui trattazione formale può essere fuori dalla portata degli studenti.
Un esempio: passeggiate aleatorie
Si consideri un semplice programma che fa avanzare il gatto di Scratch! muovendosi dalla sinistra la verso destra dello schermo, sulla base dell’esito del lancio di una moneta non truccata: se esce testa il gatto compie un passo verso destra e uno verso l’alto, se esce croce il gatto compie un passo verso destra e uno verso il basso. Questo fa sì che il gatto disegni una traiettoria (che tecnicamente rappresenterebbe una cosiddetta passeggiata aleatoria monodimensionale) a partire dalla quale si possono formulare tantissime domande.
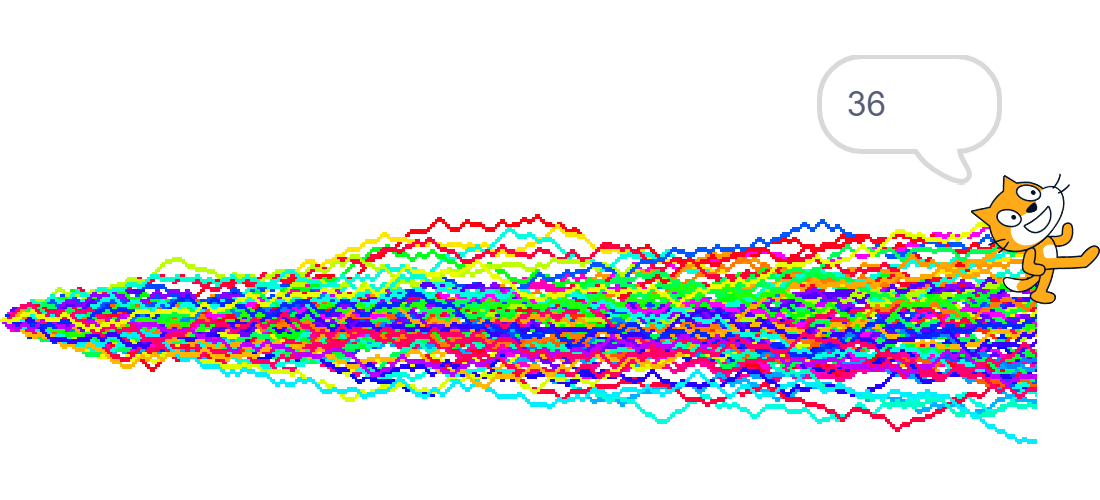
Una serie di passeggiate aleatorie generate con Scratch! a partire da uno stesso punto.
Per esempio: quando il gatto raggiungerà la destra dello schermo, di quanto si sarà scostato verticalmente rispetto alla posizione iniziale? Non è difficile accorgersi che questo risultato cambia ogni volta che si lancia il programma e dunque che è opportuno costruire una statistica degli esiti osservati, magari con un diagramma a barre per visualizzarli meglio.
E le domande possono andare oltre: in media, qual è l’esito finale che ci si può attendere con maggiore probabilità? Come cambia il diagramma se cambiamo l’ampiezza dei passi (in verticale, in orizzontale, …)? Come cambia l’esito medio che ci si può attendere se la moneta è truccata?
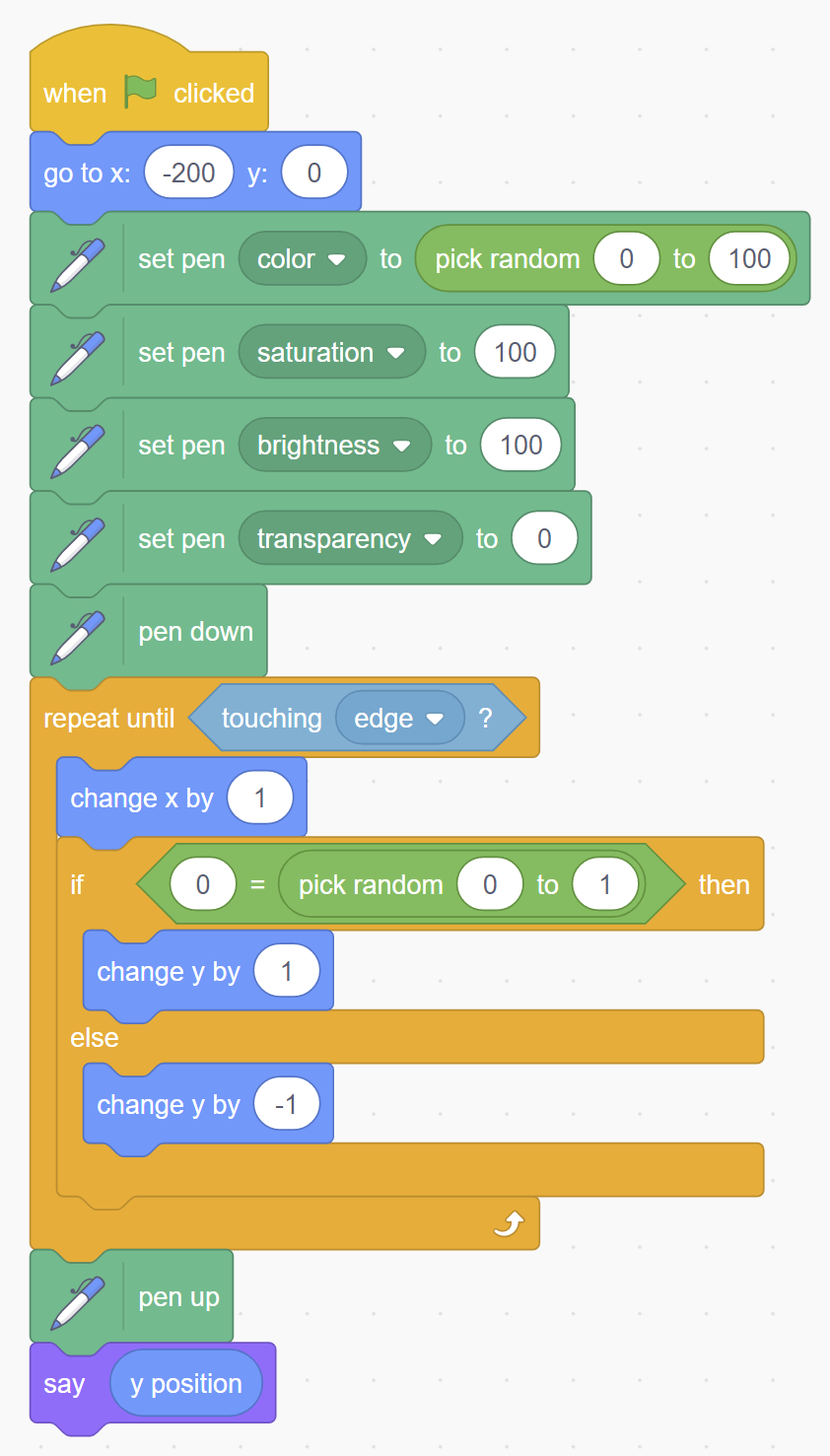
Il codice Scratch! utilizzato per generare passeggiate aleatorie.
Questo semplice esperimento nasconde un sacco di questioni probabilistiche anche molto sottili e può essere occasione per discussioni estremamente profonde. Si pensi alla fallacia dello scommettitore e quindi al condizionamento e all’indipendenza degli eventi, ma anche a diverse nozioni di probabilità (come quella classica e quella frequentista), ai concetti più sofisticati che vengono sfiorati (senza però essere insegnati) come quello di densità di probabilità, di valore atteso, di processo aleatorio, ecc.
Altri esempi
Scratch! consente di esplorare tanti altri problemi in cui la probabilità ha un ruolo.
Le passeggiate aleatorie, per esempio, possono essere anche bidimensionali (cioè il movimento casuale può non essere solo lungo la direzione verticale) e quindi avere un maggior numero di parametri su cui intervenire, facendo anche variare molto la tipologia di domande che ci si può porre (comprese quelle legate alla geometria delle trame disegnate).
Si può anche ragionare su giochi le cui spiegazioni teoriche sono alla portata degli studenti, come una semplice “gara” in cui i concorrenti avanzano sulla base dell’esito del lancio di due dadi (in fin dei conti, come succede in molti giochi da tavolo). Questa può essere l’occasione per introdurre diversi aspetti di coding, come per esempio l’invio di messaggi tra sprite e background.
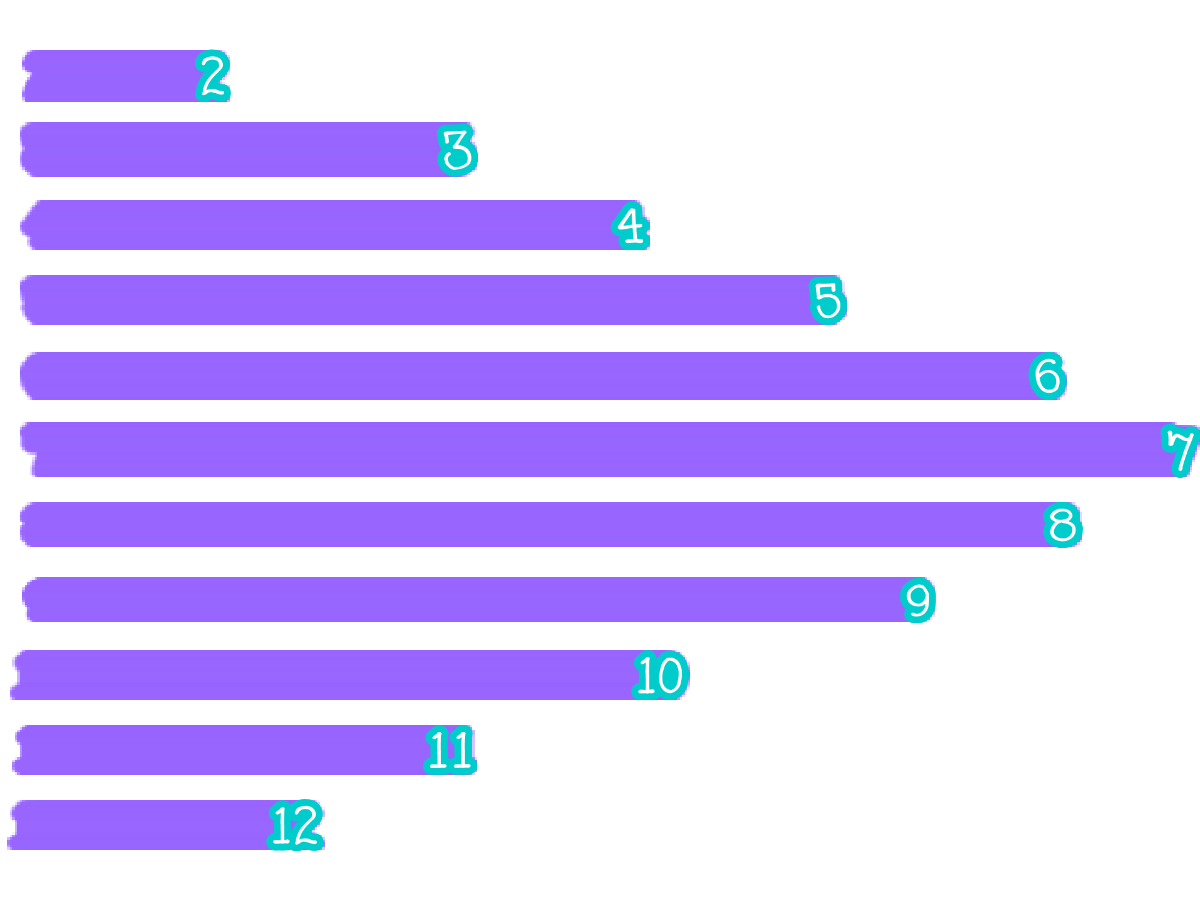
L’esito finale di una “gara” basata sulla somma degli esiti del lancio di due dadi per 2911 volte: il 7 è vincitore.
Un bell’esempio di problema controintuitivo che si può simulare in Scratch! è il problema di Monty Hall, di cui si può trovare ampia trattazione sul web e per il quale emerge chiaramente quanto a volte sia difficile per noi intuire come gli eventi probabilistici possano dipendere gli uni dagli altri.
Per chiudere, vi propongo anche di esporre gli studenti all’utilizzo di Scratch! e della probabilità per applicazioni sorprendenti, come quella della stima delle aree (per approfondimenti si vedano a questo proposito il Metodo Monte Carlo).
Tutti questi esempi possono essere visti con diverso livello di profondità, sia dal punto di vista matematico che da quello di scrittura del codice. La sfida per il docente è sempre la stessa: trovare il giusto equilibrio. Questa può essere vinta solo conoscendo bene i propri studenti e cercando di trovare, come al solito, il giusto bilanciamento. Buona ricerca a tutte e a tutti!
Per approfondire
Live streaming:
Esempi di codici con esperimenti aleatori:
- Passeggiate aleatorie monodimensionali
- Passeggiate aleatorie bidimensionali
- Number’s race
- Stima del pi greco (Monte Carlo)
Approfondimenti:


